
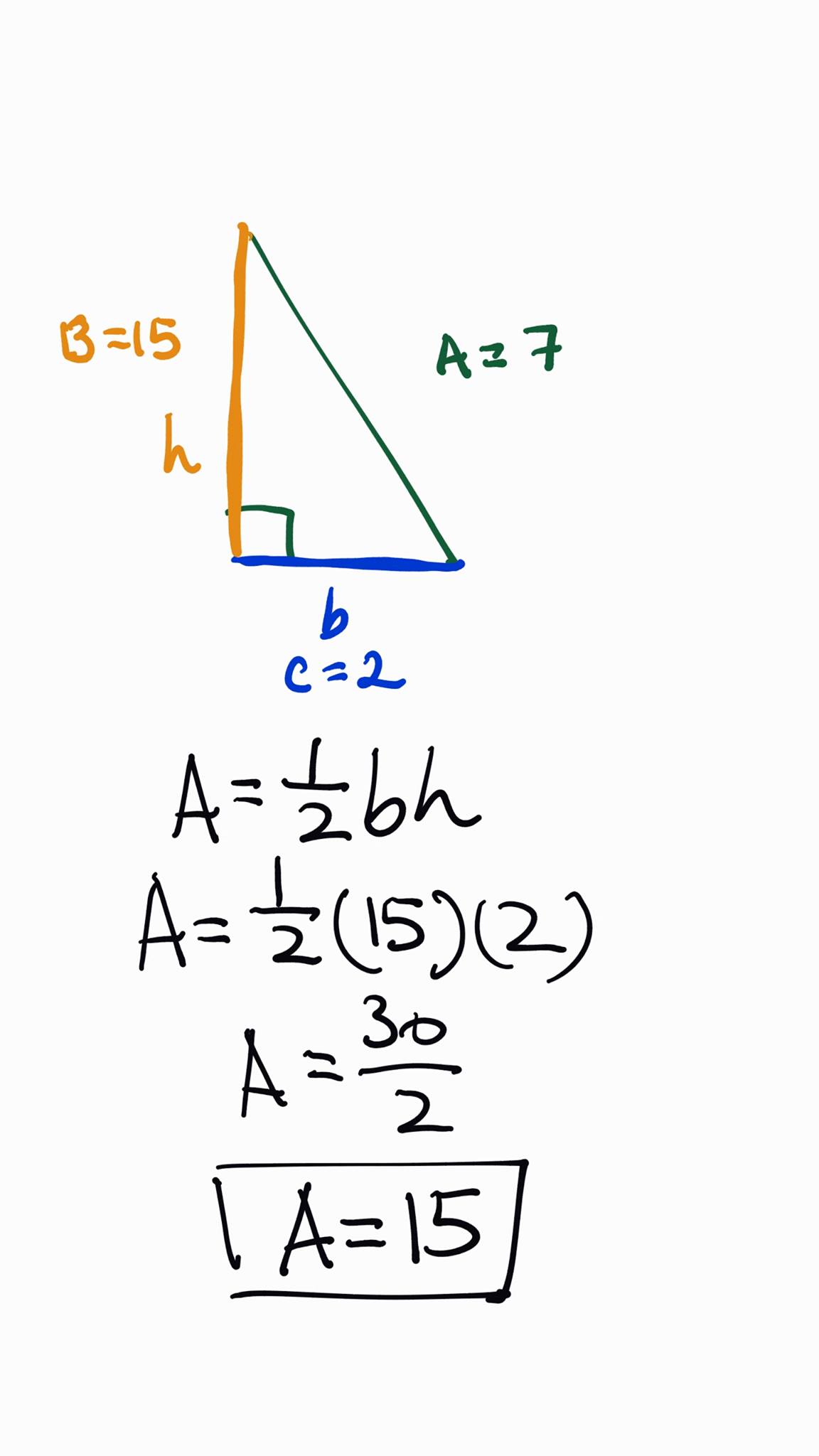
If you know the lengths of two congruent sides (a,a) and the length of the non-congruent side (c) of an isosceles triangle, you can use the Law of Cosines to find the measure of the angles. To calculate the properties of an isosceles triangle when given certain information, you can use the Pythagorean theorem, the Law of Cosines, or the Law of Sines. An isosceles triangle is a triangle where two sides have the same length. If we have a length of the hypotenuse and one cathetus, you have to enter these values in given fields, so let’s assume we have one cathetus, which is 4 meters, and a hypotenuse is 5 meters.This calculator calculates any isosceles triangle specified by two of its properties. If you have trouble with understanding of angles, then you should read this post about conversion of angles. Remember to change the units of measure to get everything in the same. We will automatically get the second leg and angle, and it will be 7.14 cm and 55 degrees.Then it is necessary to enter the angle in units of degree by entering the value 35 in the field Angle α.First, we change the units of measurement from meters to centimetres and enter the value 5 in field a.So the angle that this leg closes is 35 degrees. We have the length of one leg, let’s say, and it is 5 centimetres. Field c is automatically filled and is 12.81 m.We will select a two-length mode for the calculation so that we will make an entry: Suppose we have given two legs, the first 10 meters long and the second 8 meters long. We will use our ART calculator for calculation. If the triangle is right-angled, then the sum of the squares over the legs is equal to the square over the hypotenuse.īelow we will show some examples of calculations with different given values. Pythagoras’ theorem is the relationship in Euclidean geometry between the three sides of a right triangle. The Pythagorean theorem holds in a right triangle. Therefore, the legs or catheti are also two heights of the triangle. In a right triangle, the hypotenuse is larger than each cathetus. This is because of the opposite length, the right angle is the hypotenuse, and the other two sides are the cathetus. The definition of the right triangle is as follows:Ī triangles with one 90 degrees angle are called a right triangles. So, for example, if this triangle ABC had two 90 degrees angles, then at point C, there would be two normals on line a.

In each triangle, only one angle can be right.

While you are here, you should look at some more of our solutions and help calculate various math quantities, such as Root or Cube. Finally, we will show a concrete application of our calculator with a few examples. Furthermore, we will explain what an isosceles right triangle is and various variations of formulas. The following text will show what a right triangle is and which formulas we can use to calculate its area. As a result, the area of the right triangle is presented in the marked field. You have to choose which variation of the given values you have and then enter them in the marked fields. CalCon mobile app or browser interactive user face allows you to find the area using an interactive calculator. Here you can use our Area of the Right Triangle Calculator (ART) to calculate the area of the Right Triangle.


 0 kommentar(er)
0 kommentar(er)
